配套教材:钟玉泉.复变函数论(第四版) 其中图片均来自该教材
鉴于本章课本内容较多,单看课本顺序较难挖掘出定理之间深层关系(例如Morera定理可看做柯西积分定理所推出的两条分支的汇合),故将定理之间的逻辑关系重新整理如下。如此可发现本章内容已非常清晰。限于本人水平,难免有错误和纰漏,敬请大家指出。
关于复变函数的积分,各定理之间的逻辑关系可用下图简要表示:
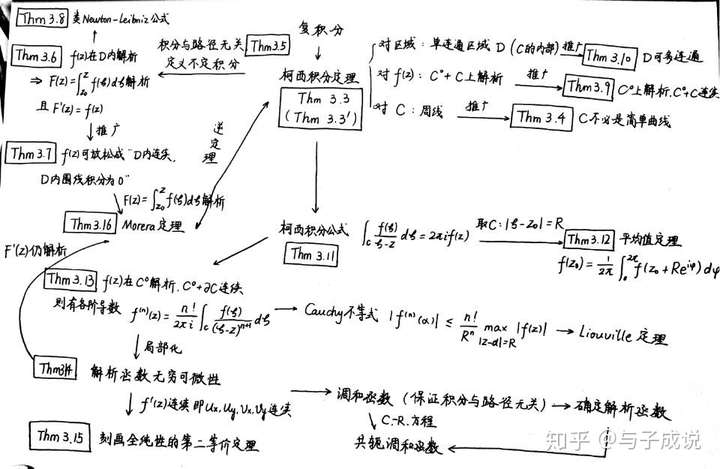
在给出复变函数的积分定义、性质及计算方法,并类比数学分析引入曲线积分、区域等有关概念,本章内容主要集中在柯西积分定理和柯西积分公式两部分。
以下讨论三部分:
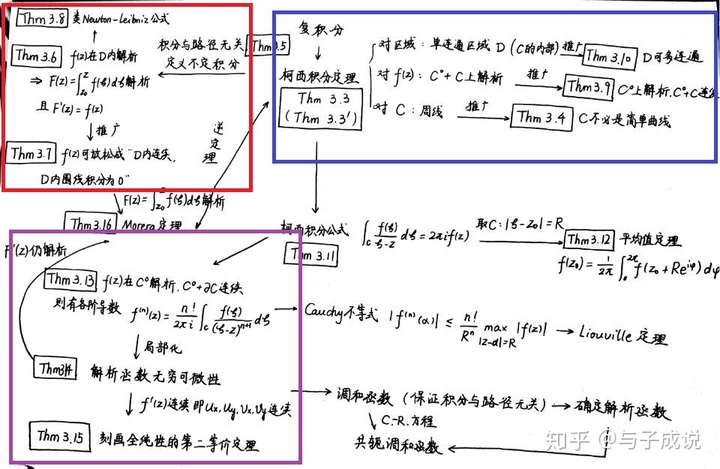
第一部分是柯西积分定理及其推广。(蓝色框)
首先给出柯西积分定理:
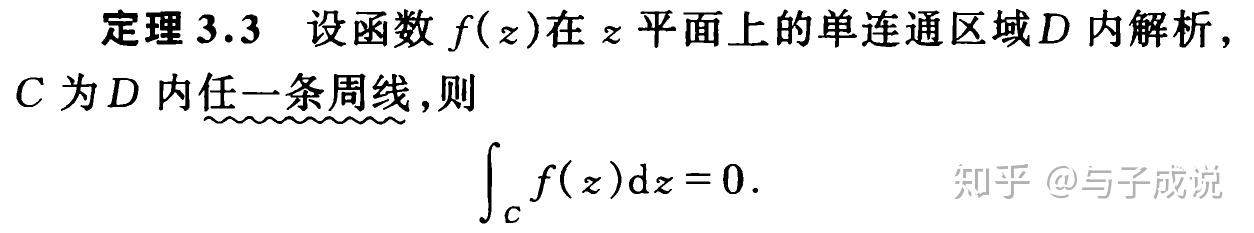
柯西积分定理是一个关于复平面上解析函数(全纯函数)的路径积分的重要定理。同时易证明还存在如下的等价定理:
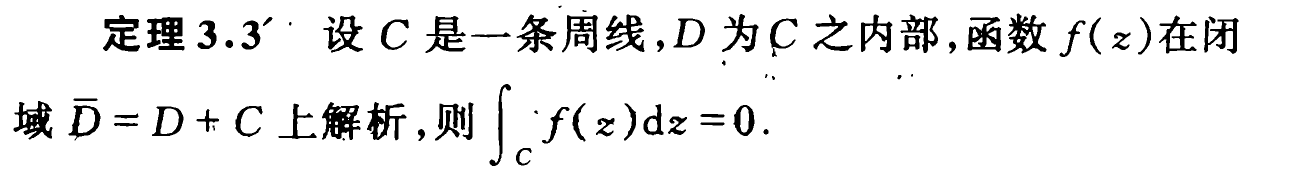
它的使用条件包含三个不同的角度:
(1)对区域:要求区域为单连通区域
(2)对函数 :要求
在
上解析
(3)对积分曲线 :要求
为
内一条周线
所以我们可以从上述三个角度对柯西积分定理进行推广,分别得到
(1)对区域的推广: 可推广为多连通区域(即边界可推广到多条周线组成的“复边界”)
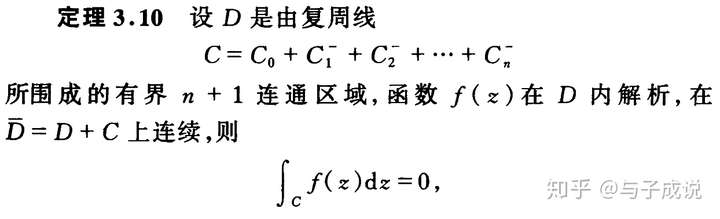
在数学分析、复变函数等课程中,每当被积函数遇到所谓的“奇点”(或更广泛一点,破坏函数全纯性质的点)时,挖小圆往往是计算含有这类特殊点的围道积分的有效方法。当外边界和内边界同取诱导定向时,我们可以得到:沿外边界积分等于沿内边界积分之和。
(2)对函数的推广:与一元函数的微分中值定理条件(闭区间连续,开区间可导)相似,我们可以把
的条件放宽成“闭包连续,内部可导”,即

(3)对周线 ,同样可以推广到“非简单曲线”的情形,即

参考积分的路径可加性,证明是容易的。
第二部分是复变函数不定积分理论。(红色框)
首先考虑一元函数的情形,构造 ,
的可积就可以保证
的连续性。然而若类似的定义
,我们会发现若
的路径积分与路径有关,如此
就不是单值函数。好在柯西积分定理给了我们“积分与路径无关”的有关结论:

这个的证明可参考数分曲线积分与路径无关的一系列等价条件。如此我们便可以定义变动上限的积分,并自然地确定
解析且能作为
原函数的条件。后续过程可参考课本定理3.6,3.7与3.8。
第三部分是柯西积分公式。(紫色框,紫色框右侧可看做柯西积分公式的推论)
顺着柯西积分定理的主线往下走,利用内含圆的思想可证明柯西积分公式:

通过柯西积分公式,就可以把解析函数在简单闭曲线的内部任意一点处的值,用边界上的值表示。柯西积分公式不但提供了计算某些复变函数沿闭路积分的一种方法,而且给出了解析函数的一个积分表达式。平均值公式(Thm3.12) 就是它的一个推论。
然而它的最主要应用还是导出了全纯复变函数各阶导数的公式

并利用小圆将这一性质在区域 上局部化,得到了解析函数又一非常美丽的性质——解析函数的无穷可微性:
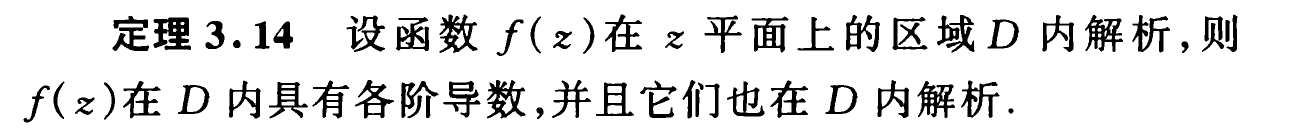
考虑 的连续性,我们立刻得到了刻画解析函数的第二个等价定理:

在这里需要指出的是,借助全纯复变函数各阶导数的公式,我们还可以得到柯西不等式

需要特别说明的是,在这里
上的最大模和
上的最大模是等价的,这里需要用一下后面的内容,即解析函数的最大模原理,也就是边界上的最大模实际上是限制住了内部的最大模。
后面借助柯西不等式给出了刘维尔定理,并用它很轻松地证明了初等方法难以证明的代数基本定理。此条支线暂时结束。
【终章】两条支线的最终会和——Morera定理
我们欣喜地看到,复变函数不定积分支线和解析函数无穷可微支线汇合到了一起,复变函数不定积分支线提供了 的解析性,而解析函数无穷可微支线提供了
的解析性,最终得出了Morera(莫雷拉)定理:
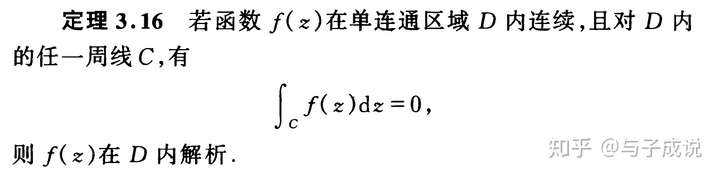
这个定理也给了我们又一个解析函数的充分必要条件:

【注】至此我们已得到了解析函数的三个等价条件,他们分别是定理2.4,定理3.15和定理3.17 。
从柯西积分定理这个基础出发,它延伸出的两条分支最终汇合,证明了柯西积分定理它自己的逆命题,这算不算一个很圆满的结果呢?
再者就是调和函数、共轭调和函数与解析函数之间的关系。我们可以看到调和函数结合Green公式在解析性的证明过程中发挥了重要作用,共轭调和函数这一概念也是连接实域调和函数和复域全纯函数的有效桥梁。这条线后期独立于本章主线,故仅到此为止。
完。限于本人水平,难免有错误和纰漏,敬请指出!