物理学：知乎上找到的一个系列文章——《Halbach array 的构建与模拟》

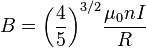
知乎上找到了一个系列文章——《Halbach array 的构建与模拟》，一共写了三篇，链接分别如下：

1. Halbach array 的构建与模拟（一） – 知乎 (zhihu.com)
2. Halbach array 的构建与模拟（二） – 知乎 (zhihu.com)
3. Halbach array 的构建与模拟（终极版） – 知乎 (zhihu.com)

以下是全文转载。

Halbach array 的构建与模拟（一） – 知乎 (zhihu.com)

写在前面：

好久没有刷知乎了，此前有一段时间知乎刷地如痴如醉，每天打开知乎APP的次数的已经超过了微信。过多的沉迷于知乎而产生的负罪感让我感到内心的空虚。可是，这东西就像吸毒与自慰一样，很难戒除。直到看到一句话：

是的，吾生也有涯，长期以来困扰我的两问题一个是我喜欢的女生不喜欢我，一个是时间太少而想学的东西太多，而知也无涯。与其一团浆糊的死去，不如让脑子的熵减低那么一点点，让世界的信息有条理一点。

第一个问题暂且不讨论，第二个问题真是戳中了我的痛处。对啊，想学的东西太多了，高中的时候我就想博览群书，学习广泛学习计算机知识，那时候很喜欢天文，想把天上星星都认全了。可是，直到现在我都没有读过几本书，也没有自学各种计算机操作知识，也没有认识几颗星星。大学快结束了，我还一直沉迷在各种碎片化的信息，浪费着我的时间，腐蚀着我最初的梦想，换取的只是浮名而已。拖延症很难改掉，我不改掉不会影响世界的运转，历史告诉我们人类社会成功者与loser的比例是几乎不变的，我一直拖延着大不了成为下一个loser而已罢了！

今天朋友发过来一条消息（美国科学院士蒲慕明给学生的一封信）意思是，作为科研人，如果你每周工作5天每天8小时还能取得什么重大成功的话，那世界上所有的幸运都会属于你了。

科研，拒绝拖拉。

正文

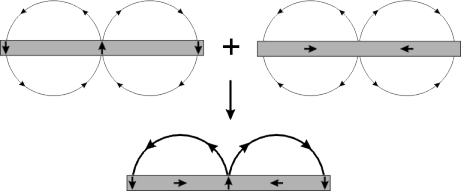
简单介绍Halbach Array（海尔贝克阵列），就是一种磁体结构。可以理解为用永磁体排成阵列，通过叠加产生我们需要的磁场。通过不同的排列可以实现各种磁场分布。1979 年，美国学者Klaus Halbach做电子加速实验时，发现了这种特殊的永磁铁结构。下面是几个简单的排布（来自Wikipedia）

 

上面这个的排布，箭头表示磁铁磁化方向。这个阵列，下方磁场很强，上方磁场相互抵消，具有单面磁铁性质（一面磁性很强，一面磁性很弱）。下图用叠加性形象说明了此种Halbach的特性，下方的磁感线抵消，上方增强。

 

对了，一些排列磁铁会排斥，强势固定就可以了。磁感线相互叠加的地方，磁感应强度（也称磁通密度 ）B会增大，磁场具有的能量会增大，根据系统稳定时最低能量原理，产生排斥力。,磁能密度，总能量积分即可。

 

 

知识储备

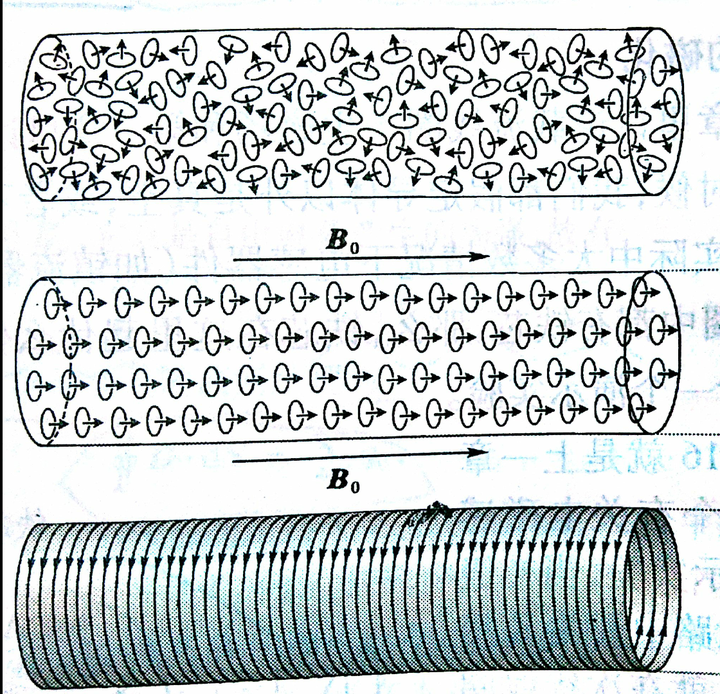
用安培分子电流模型解释磁化强度。组成磁介质物质的基本单元看成环形电流，这模型有一定的道理，按照经典描述，物质原子中的电子围绕原子核运动产生电流。有电流就有磁矩，，a是电流环的面积，磁矩方向遵守右手螺旋关系。没有加磁场时，介质中的磁矩随机排列，相互抵消，对外不显示磁性。当外加磁场时，磁矩产生力矩，磁矩最终会旋转到与磁场方向平行，此时能量最低。如下图。介质内部磁化电流抵消，只有在表面电流未抵消，磁化电流组成的螺线管产生的与磁化场方向一致。所以磁介质内部总比没有磁介质时的增大了。

 

磁化强度,,可以反映出磁化介质磁化状态的矢量。

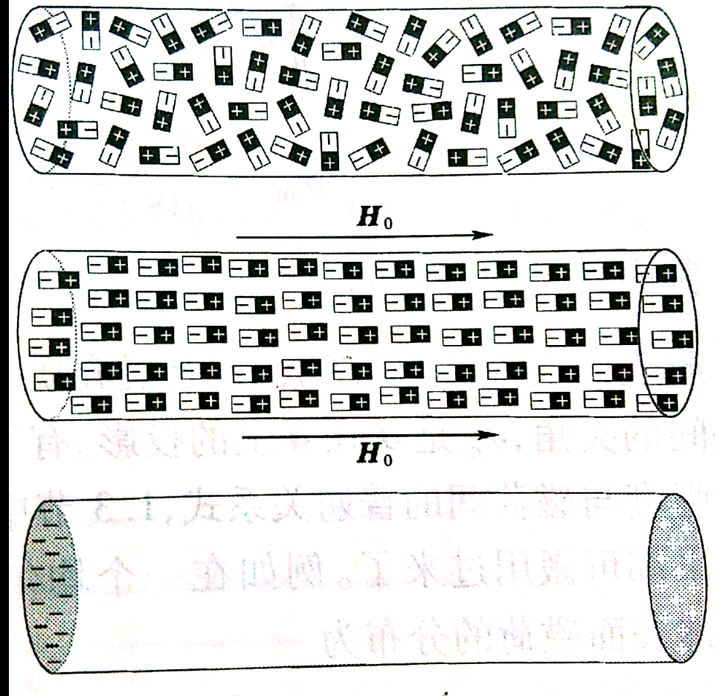
大体说一下磁荷观点。历史上，磁的理论起初建立在磁的库仑定律基础(与电荷库仑定律类似，知识把电荷改成了磁荷，系数换了一下)上。磁荷观点，磁介质最小单元是磁偶极子，我们知道电偶极子就是一正电荷与负电荷组成的体系，那么磁偶极子也差不多，两个反极性的磁单极子组成（假设），类比小磁针。如下图，当加入外界磁场，磁化场将每个磁矩分子产生一个力矩，使磁偶极矩转向磁场方向。内部相互抵消，宏观效果是两端产生N,S极或者说正负磁荷。注意到，附加磁场与磁化场方向相反，介质内部总的是减小的。称为退磁化场。

 

一个小磁针的外部磁场分布与一电流环产生的磁场分布一致。如下图：

 

故，磁荷观点与分子电流观点等价。

真空中存在外界磁场,当空间多了一磁介质时候，磁介质内部空间是增大的，是减小的。满足，（注意这儿的是空间某一点总的磁场强度）其中，，为磁化率，是介质的相对磁导率。

磁介质的分类：

电介质中，极化强度，，并且对于大多数电介质，是与场强无关的常数。而在关于磁，情况比较复杂。磁介质分为顺磁介质，抗磁介质与铁磁介质。对于顺磁介质，，相对磁导率大于1；对于抗磁介质，，小于1。顺磁介质与抗磁介质磁性都很弱，，，且与无关。抗磁性比顺磁性介质更接近1。

对于铁磁介质，与不成比例，且没有单值关系。脑补一下著名的磁滞回线，一个对应两个，磁化率还与“磁化的历史”有关。与呈非线性关系，，铁磁介质的一般很大，一般是，甚至能到。

进一步了解

抗磁性产生由于电子在外部磁场做拉莫尔进动，由于电子带负电，电子拉莫尔进动产生的磁场与磁化磁场相反，产生抗磁性。

抗磁性的长生是磁场对电子轨道运动的作用结果。所以，抗磁性具有普遍性。

顺磁性 ：当原子具有磁矩时（），原子磁矩在磁场取向是量子化的，不同的取向对应不同的附加能量，平衡时遵从玻尔兹曼分布，处于不同能级的原子数与成正比。能量低的原子比能量高的原子数目多，也就是与夹角小于90°的原子数目占绝大多数，所以物质显出顺磁性。由这个模型还可以推知居里定律：顺磁性物质磁化率同绝对温度成反比。感性认识一下：当温度很高时，由玻尔兹曼分布知道能级差别不是很明显了，所以磁化率降低。当温度降低时，热运动减弱，磁矩自发平行排列（能量最低原理），自发磁化，顺磁物质转化为铁磁物质，这个过程是二级相变，临界温度称为居里温度。其实可以说，顺磁与铁磁的相变，就是无规则的热运动与有序的磁场力相互竞争的过程。

对于的原子，只有抗磁性存在。注意，宏观物体的磁性不一定等于原子的磁性，由分子构成的物质磁性决定于分子，固体的磁性还于固体结构有关。

铁磁物质：

Fe，Co，Ni等及其氧化物在受到外场磁化时，显出比顺磁性物质更强的磁性，失去外界磁场时，还保留磁性。铁磁物质的原子具有磁矩，这类原子之间又发生自发磁化作用，在一个小区域原子磁矩沿着一个方向排列起来，形成较强的磁矩。在局部，已经很强的磁化了，这样的小区局部称为磁畴，每个磁畴各有不同的取向，且磁畴交界处阻力较大，当有外界磁场时，磁畴的磁矩向外磁场方向转动，这样才对外显出较强的宏观磁性。

铁磁分类——(1).软磁材料，矫顽力小，磁滞回线包围的面积小。(2).硬磁材料（永磁体）必须有较大的矫顽力Hc，此外还要有较大的磁能积（BH）。钕铁硼合金最好的永磁体。

解释铁磁体自发磁化：

在有些物质里，由于一种称为交换相互作用（exchange interaction）的特别量子力学效应，自旋与自旋彼此之间方向的改变，会导致临近电子静电排斥力的改变。在近距离，交换相互作用会比偶极-偶极磁相互作用强劲很多。因此，对于铁磁性物质，临近电子的自旋趋于指向同样的方向。

根据泡立不相容原理，两个自旋相同的电子不能占有同样的位置。因此，两个临近原子的位于最外电子层的不成对价电子，当它们的轨域相互重叠时，假若自旋方向相同（平行自旋）——空间波函数反对称———则电荷分布会比较分散，否则，电荷分布会比较集中。所以，促使自旋方向相同这动作会降低电势能，使得平行自旋态更为稳定。简言之，因库伦力而互相排斥的电子，借着平行自旋使得电荷分布更加分散，从而降低电势能。这能量差称为交换能（exchange energy）。

 

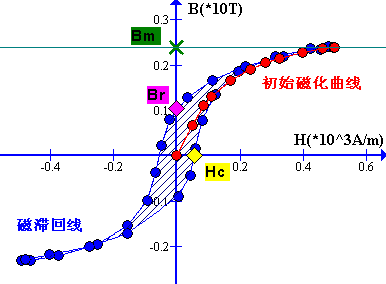
磁滞回线：

 

由于铁磁质中M的数值比H大的多，所以B-H曲线和M-H曲线差不多。

当铁磁介质的磁化达到饱和之后，去掉磁化场（），介质磁化状态不是回到起点O，而是保留一定的磁性。通常用和表示剩余磁化强度和剩余磁感应强度（，为0，所以，）。使介质完全退磁所需要的反向磁化场的大小，为矫顽力。

 

好了，关于磁铁的内容就写这么多，文章最后给一个简单的顺磁，铁磁磁化的模拟图。用Comsol静态磁场模块进行模拟。

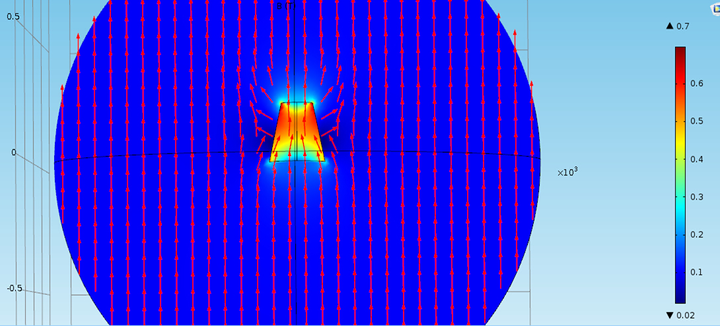
圆台tip，下底直径230nm，上底直径130nm，高230nm。外部为空气，材料属性设置为顺磁物质相对磁导率6000.环境磁场=0.1T，沿z轴正方向。求解域为球体。

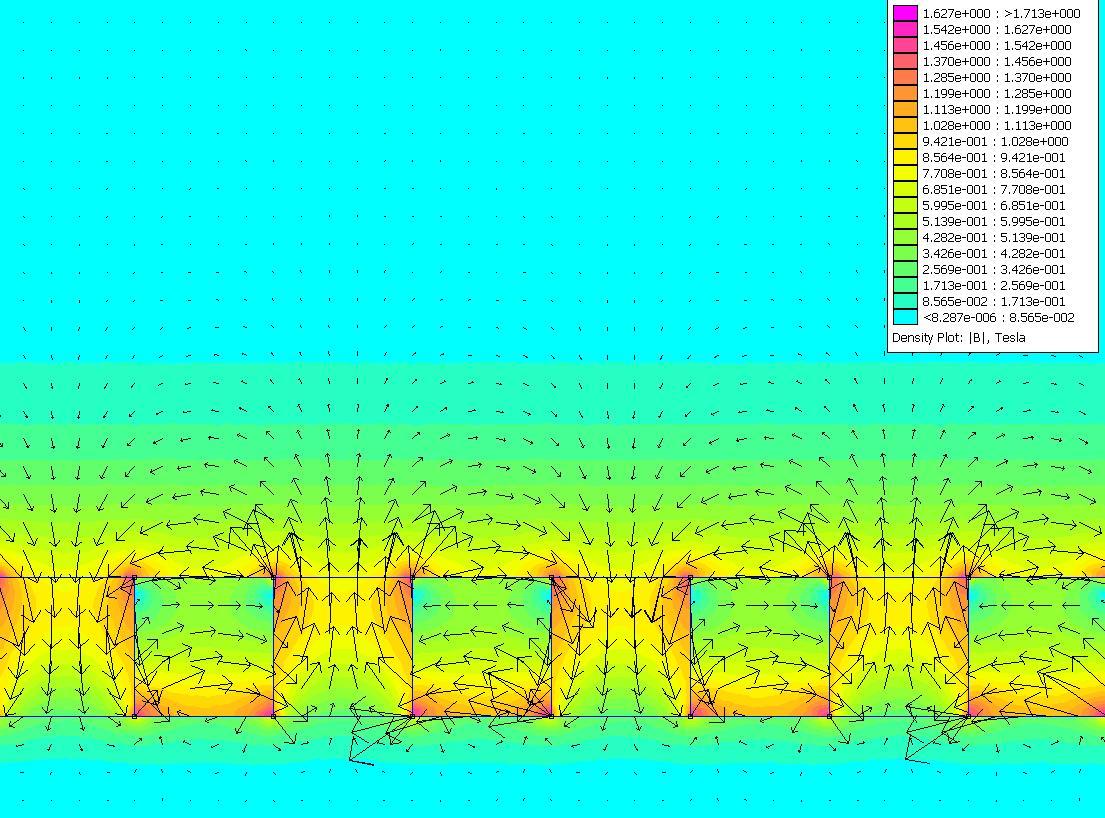
B模：

 

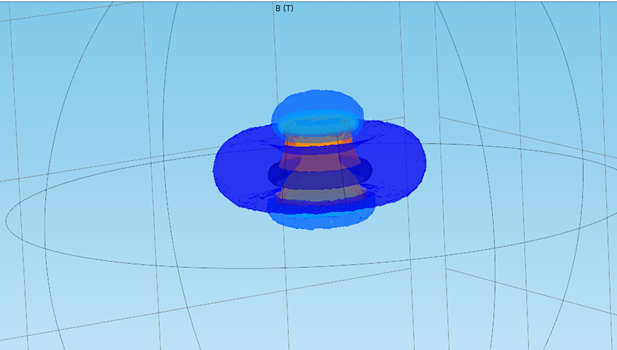
B模等值面

 

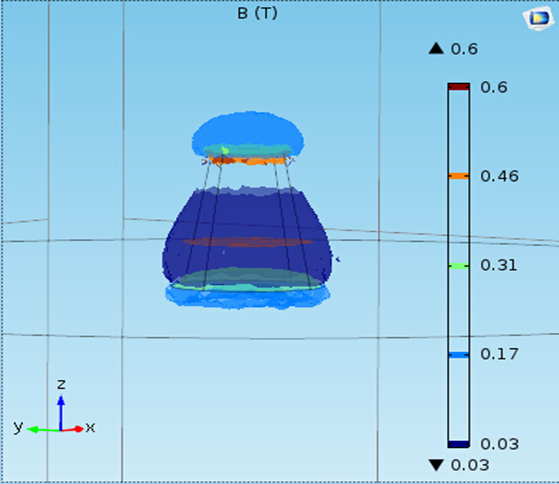
对铁磁介质进行模拟时，非线性，采用内插函数。本构关系设置为HB曲线，一样的额外部环境。下图，B模深度图：

 

B模等值面：

 

2015.3.24

深夜。By：GMS

Halbach array 的构建与模拟（二） – 知乎 (zhihu.com)

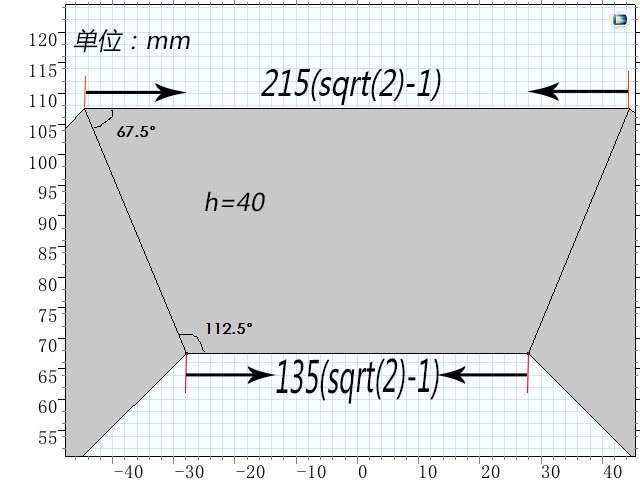
如下图是ｘｙ平面的投影，（单位ｍｍ）箭头表示磁化强度M的方向，梯形钕铁硼（型号Ｎ５０）拼接而成，其中梯形高40mm，厚40mm。钕铁硼剩磁Br=1.45T。（计算M=1.154*10^6A/m）

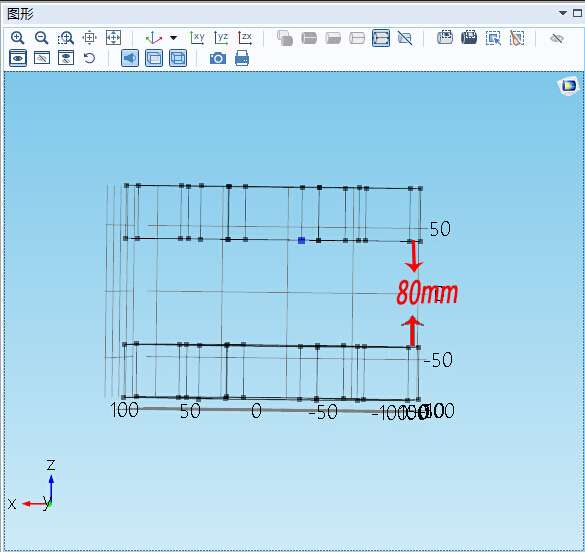
为了实现Ｂ方向的控制，将两个阵列排成如下图，相距8０ｍｍ。试图通过旋转实现Ｂ大小和方向的改变。
目标：Ｂ的大小控制０.２Ｔ左右。

 

磁化方向：

 

 

当上一个阵列旋转时，有三种方法可以模拟（稳态磁场模块，瞬态磁场模块，旋转磁模块）。我进行的工作是依然选择稳态磁场模块，在[研究]中，加一个[参数化扫描]，参数为上面阵列旋转的角度a，初始值为0度，末值为360度，步长5度，共扫描73次，最后生成gif动态图片。z=0平面的变化，箭头粗细表示B的大小，方向就是B的方向，箭头起点表示该点。俯视（不支持gif，呜呜）

 

那看几张代表性图片。

0°

90°

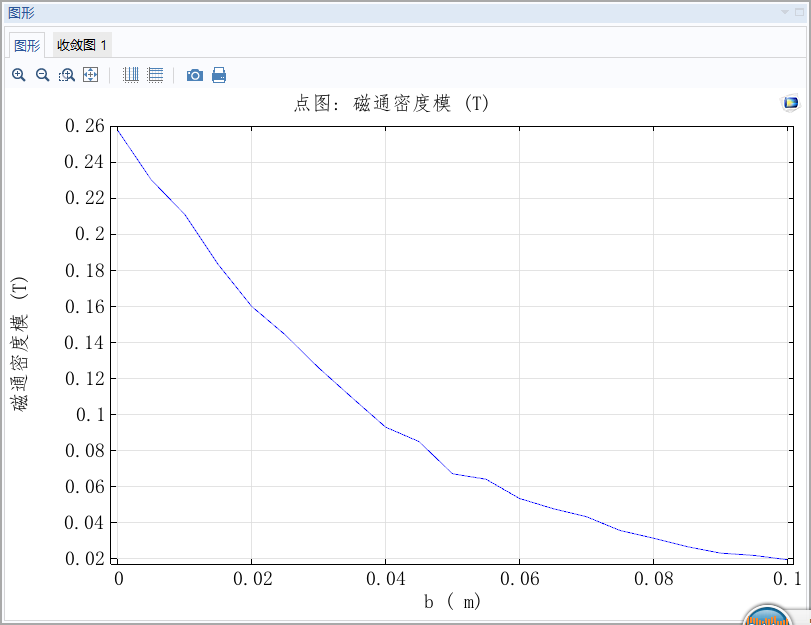
点（0,0,0）随着角度a的变化，B模变化曲线：

 

沿着z轴B模变化曲线：

 

磁感应强度B模大小还没有达到目标，下面尝试缩短阵列间距为40mm。

z轴：

 

（0,0,0）

（20,20,0）

 

（50,0,0）

其实用comsol模拟，很容易出错。以上数据是经过反复核对结果。

 

我还远没有掌握有限元分析。

By GMS 2015,3,24 早

Halbach array 的构建与模拟（终极版） – 知乎 (zhihu.com)

在许多物理实验中需要用到稳定强度高并且磁场大小在一定范围内可调节的磁场，比如粒子加速试验。

一般是用亥姆霍兹线圈，见亥姆霍茲線圈。

 

图（一）

稳定磁场为：

 

但是，由于实验室电压不稳定，比如深夜电压就比平时略大一点儿，并且方向也不太容易调节。

 

所以，我们选取永磁体阵列Halbach array（海尔贝克阵列）。通过运用特定磁体排列方式运用叠加原理可以实现特定的磁场。比如Halbach cylinder，我们翻译成“魔环”，如下图：

 

图（二）
箭头表示为磁环强度或者剩余磁感应强度的方向。

我们可以通过阵列的嵌套实现方向的改变。比如下图。俯视图：

 

图（三）

魔环内部放置一个圆环，剩余强度方向为轴负方向。

侧视图：

 

图（四）

通过转动与相对移动可以实现两个魔环内部一点磁场大小与方向的变化。

但是，有一种效应称为“退磁效应”。当磁体受到外部磁场、碰撞、温度改变等环境因素时，磁体内部的磁畴会发生变化，进而影响磁体的。比如当外界磁场与磁体剩磁不共线是时，磁畴发生转动，从而降低剩磁强度。

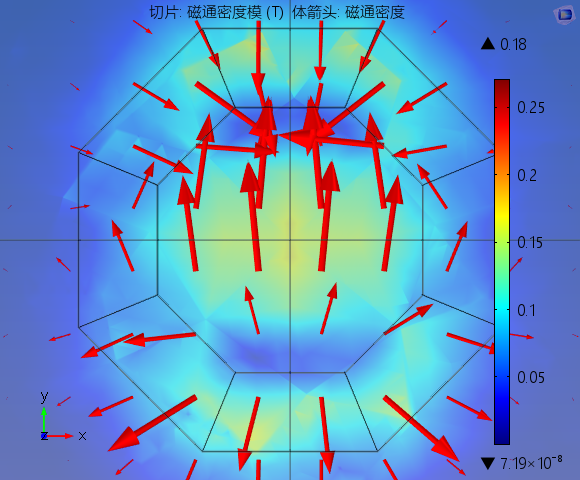
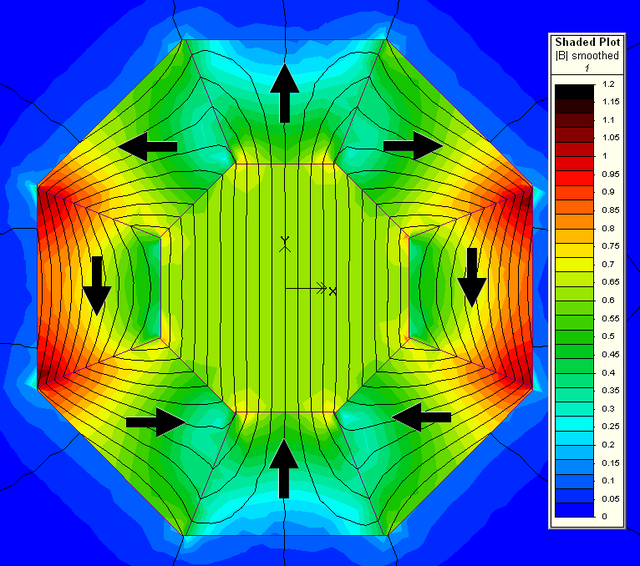
只考虑魔环，模拟结果魔环内部磁通密度方向指向轴，且为匀强磁场。外部产生的磁场很弱。为了尽可能较小由于退磁效应带来的误差和方便上下移动与转动（As the outside field of a cylinder is quite low, the relative rotation does not require strong forces.），我们将结构优化为：

 

图（五）
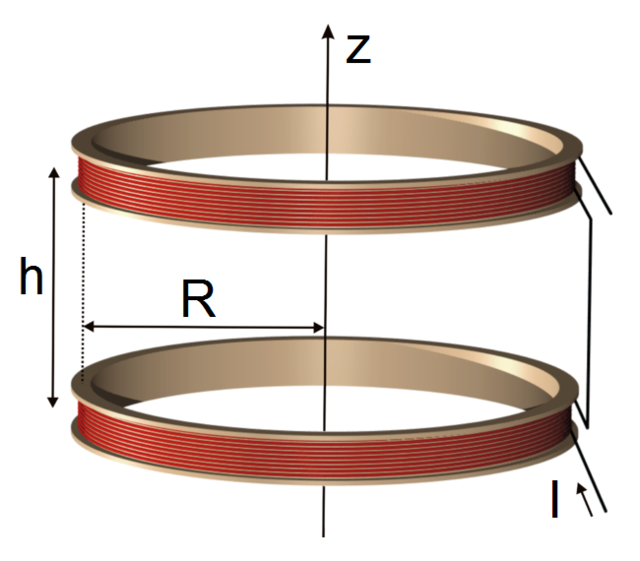
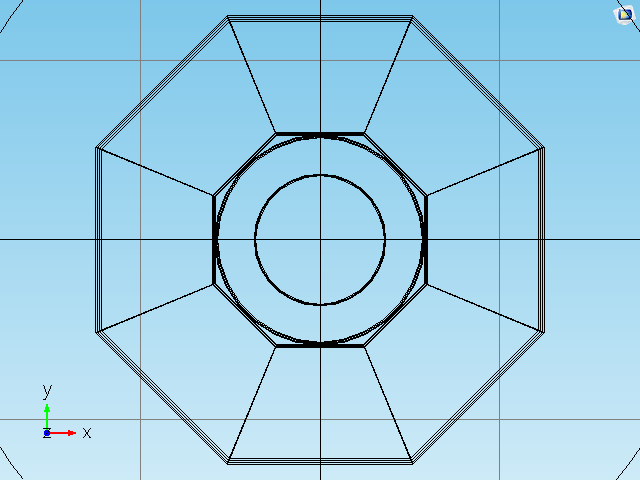
模型参数为：

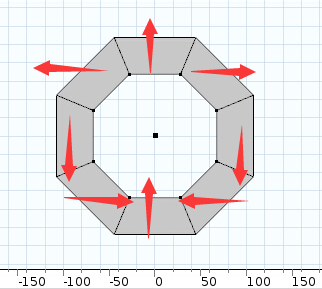
• 魔环是由八个梯形组成的正八边形。内八边形边到中心点的距离为，梯形。
  

  

  图（六）

 

• 外部圆环内径，外径。
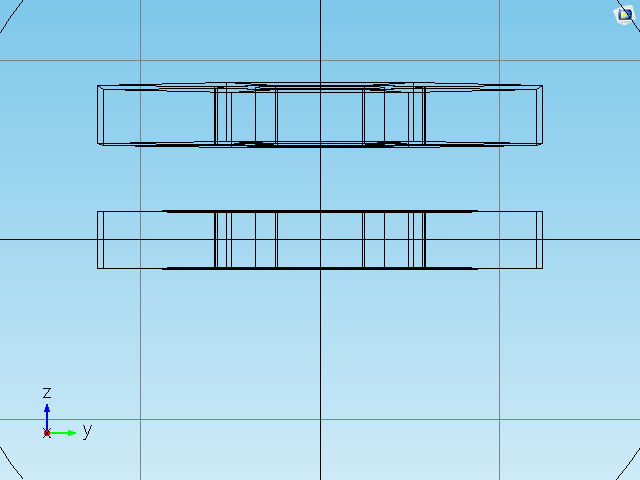
• 为了能实现磁场大小方向同时调节，还需要一个完全相同的阵列。两个阵列可以自由在轴相对移动。见图（四）。

选用矫顽力较大、剩磁强的钕铁硼N50永磁体。为。这样构建的阵列性质比较稳定。

图（七）

分析：

1.只考虑魔环，利用前面两篇的基础。

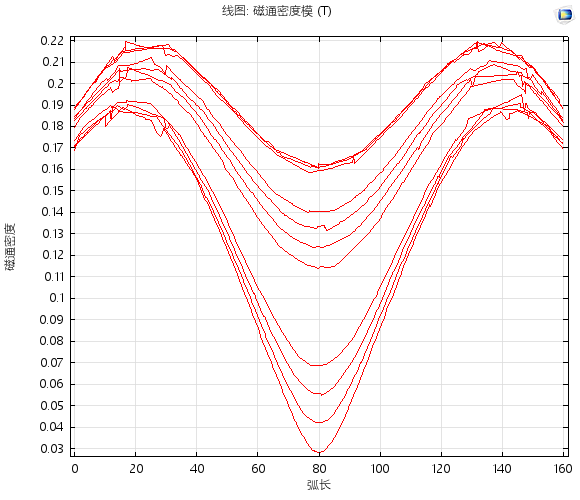
1.1对称轴上磁通密度模如下图：

图（八）

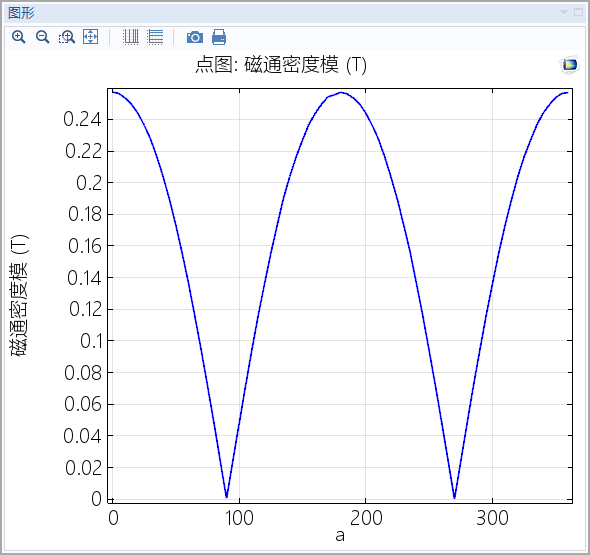
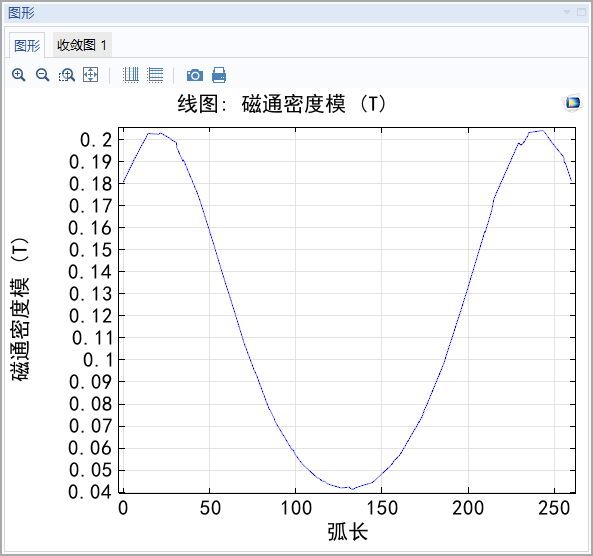
发现，两个魔环间的沿着轴，对称轴上的变化曲线为：

图（九）
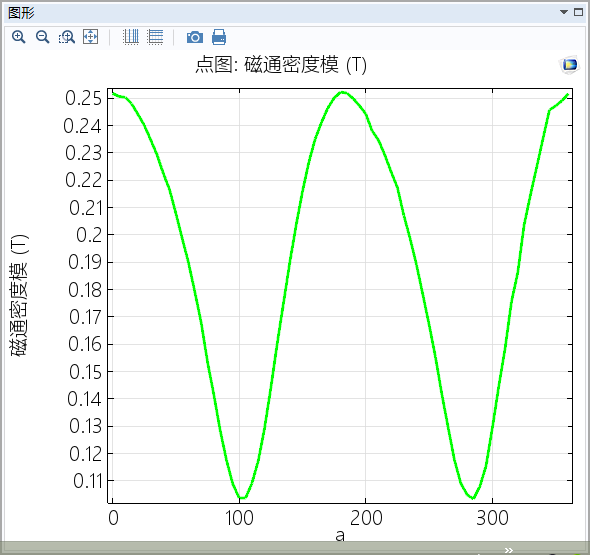
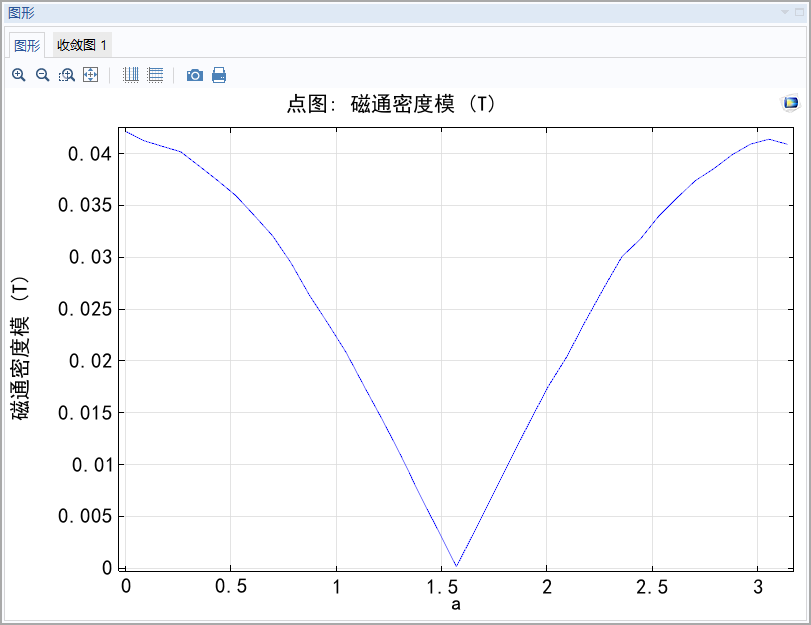
1.2固定下面的魔环，转动上面的魔环，对称中心的变化为：

 

图（十）

 

文章不支持gif，直说结论：当转动上面魔环时，两个魔环内部的磁场强度仍然在平面。大小变化如上图。

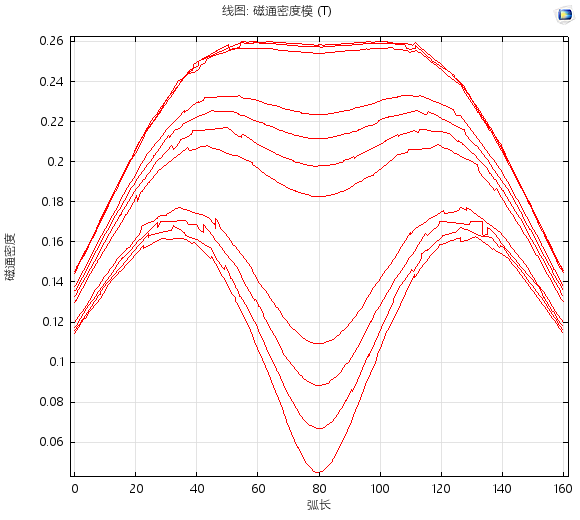
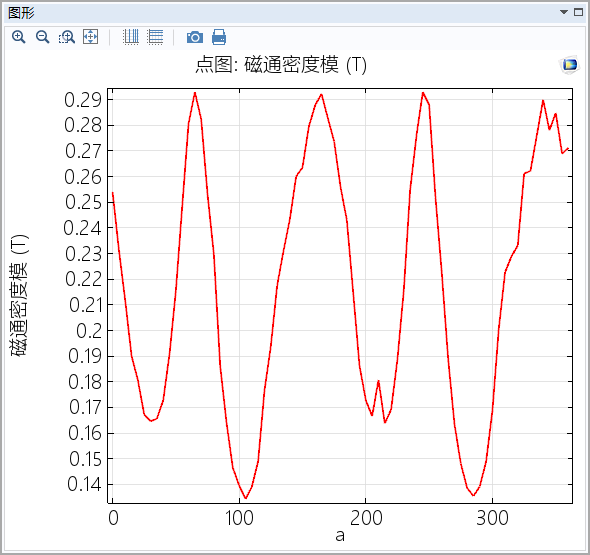
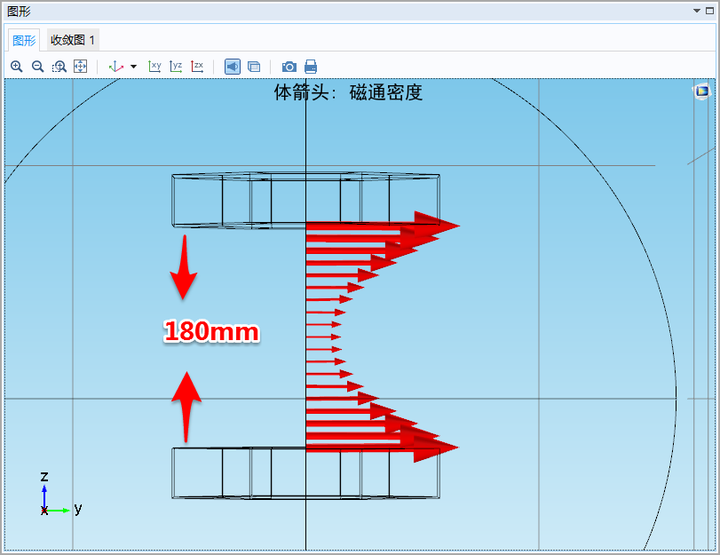
1.3 当两个魔环间距变化时（移动的过程始终与平面对称），两个魔环中心对称点（0,0,0）磁场变化为：

ps：横坐标很奇葩，起始点的原因。起点两个魔环相距

图（十一）

图（十二）

 

conclusion：通过上下移动与转动魔环，可以实现磁场在平面大小与方向的改变。

2.只考虑圆环。圆环与魔环厚度一致为。磁化方向为轴负半轴。对称性分析知，圆环体对称轴处的 磁通密度方向沿着轴。大小可以通过相对距离来调节。

3.通过叠加原理，理论上我们就可以实现阵列内部一点磁场强度与大小的变化。

 

原创。

BY——头文字D

2015/4/7